Back to: Algebra 1
To add or subtract polynomials first use the commutative property to group like terms then use the distributive property to add or subtract them.
Example: Add the polynomial expressions, (2x + 3y) + (4x + 2y)
We add as we normally do in arithmetic.
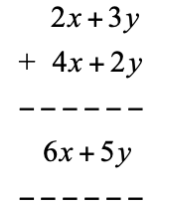
Example: Add the polynomial expressions, (3x2 + 5x + 2) + (2x2 + 3x + 6)
Again, we add as in arithmetic

Example: Subtract the polynomial expressions, (6x2+ 7x + 8) – (2x2+ 3x + 4)
Since we are subtracting all the signs in the second parenthesis change to the opposite sign.
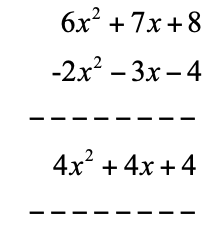
Example: Subtract the polynomial expressions, (5x2 + 6y2 – 2x + 3y + 4) – (2x2– 4y2 +2x + y – 3)
Again, all the signs in the second parenthesis change to the opposite sign.
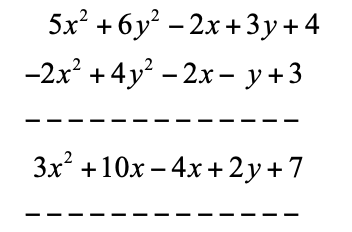
Practice Problems
Add or subtract the following polynomial expressions.
- (5x2 + 3x – 4) + (4x2 – x – 2)
- (2x3 + 4x2 – 3x – 5) + (3x2 + 6x + 7)
- (6x3 – 4x2 + x – 9) – (2x2+ 3x + 4)
- (5y2 – 3y + 8) – (2y2 + 3y + 4)
- (2x + 4xy + 3y) + (3x – 2xy + 5y)
- (x2y + 3xy2 – 2x + 3y) + (4xy2 + 5x + 2y)
- (4x2y2 – 3xy + 2x – 4y) – (-2x2y2 + 5xy + 6x – 9y)
- (8x3 + 5x2 – 2x – 5) + (-3x3 – 2x2 + 7x + 2)
- (12y4 + 8y3 + 5y2 – 6y – 3) – (7y4 – 2y3 + 6y2 – 2y + 4)
- (10x2 – 3x2y2 + 6xy – x – y) – (5x2 – 2x2y2 – 2xy + 3x + 5y)
