Unknown Angles Exterior – Triangles

Back to: Geometry

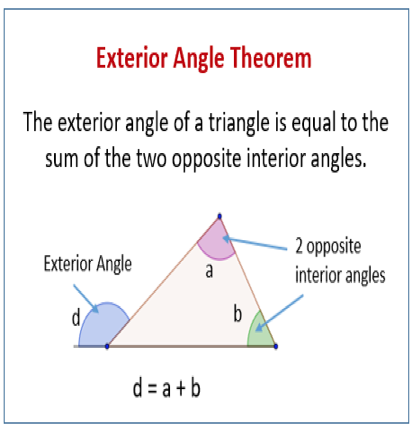
An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side.

1. The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
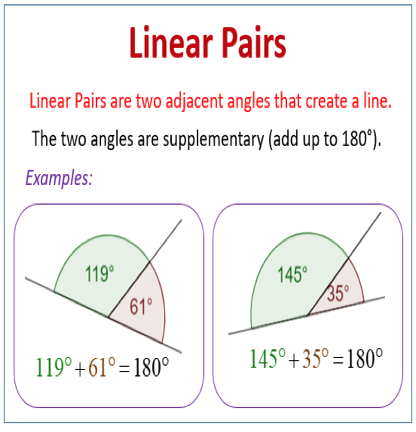
2. The exterior angle and the adjacent angle next to it form a Linear Pair (sum to 180⁰). 

Example 1

Find the value of the missing angles.

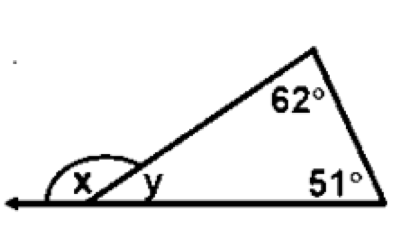
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.

Therefore, x = 62⁰ + 51⁰ = 113⁰.

The exterior angle and the adjacent angle next to it form a Linear Pair (sum to 180⁰). 

Therefore, x + y = 180⁰. Then, y = 180⁰ – 113 = 67⁰.

Example 2

Find the value of the missing angles.

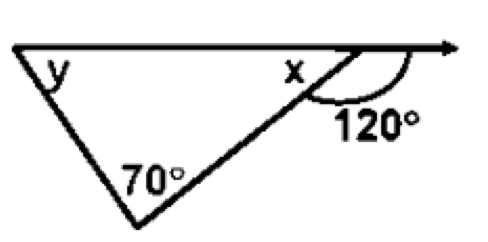
x = 180⁰ – 120⁰ = 60⁰.

y = 120⁰ – 70⁰  = 50⁰.

Example 3

Find the value of the missing angles.

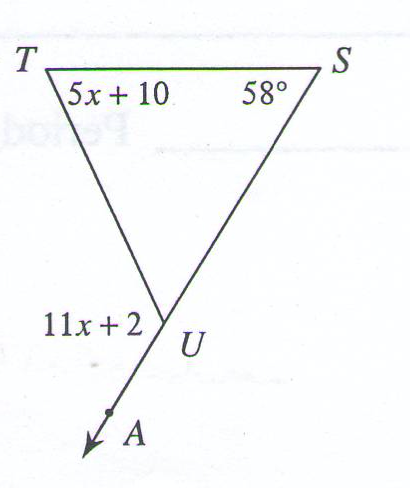
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.

Then, 11x + 2 = (5x + 10) + 58

    11x + 2 = 5x + 68

    – 5x  – 2 = -5x   – 2

    ———————–

            6x = 66

  x = 11

Therefore, 11x + 2 = 11(11) + 2 = 123. (angle AUT)

Also, 5x + 10 = 5(11) = 10 = 65 (angle T)

And 180 – 123 = 57 (angle TUS)

Solve the following problems.

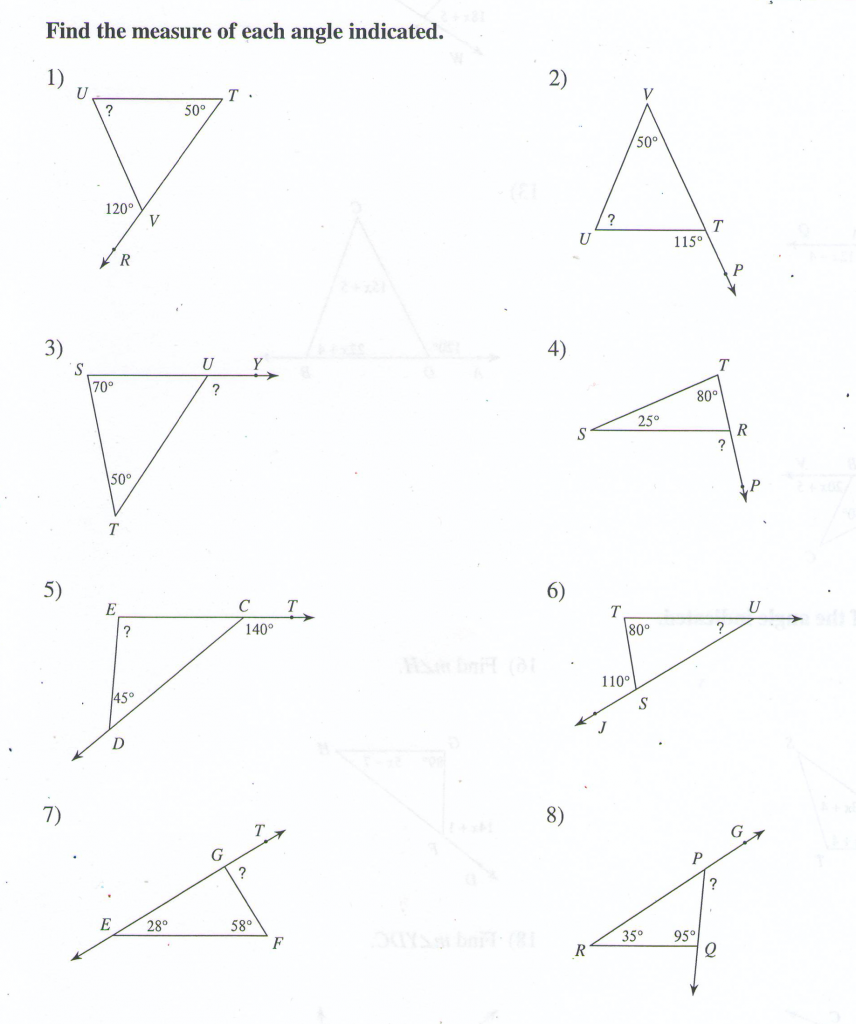
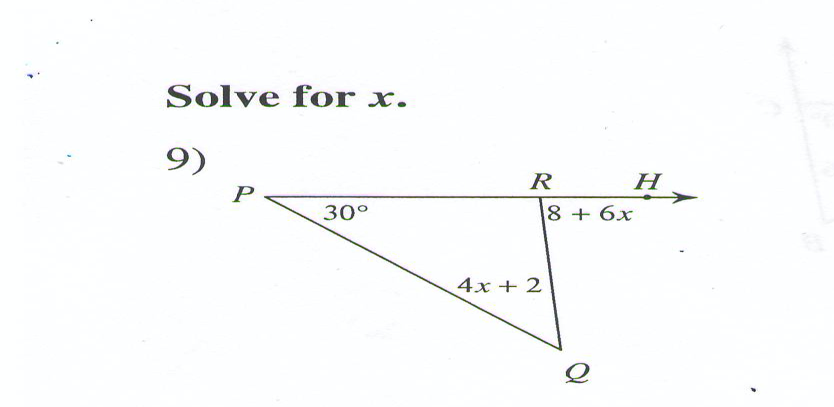
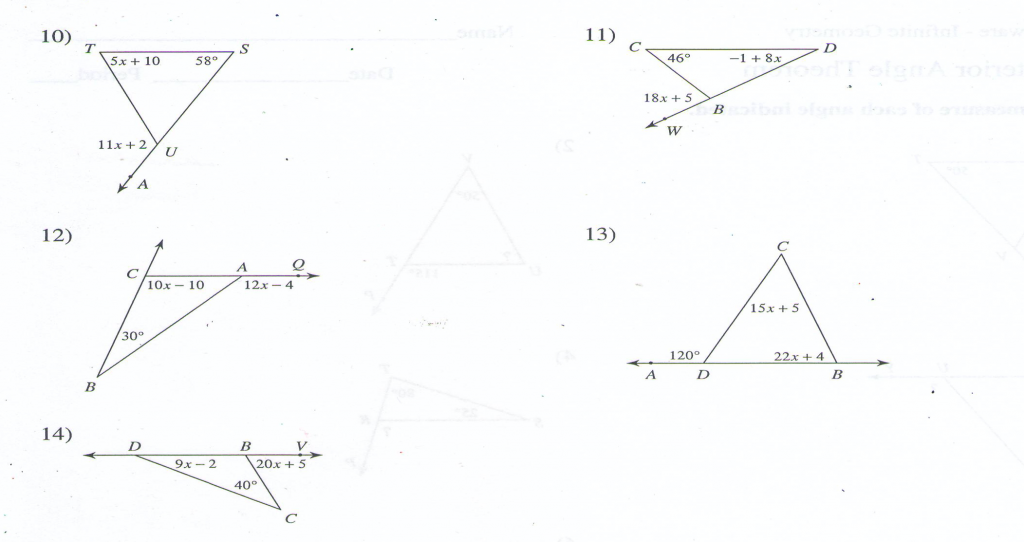
Solve for all the missing angles.

SOLUTIONS

1. 70⁰ 
2. 65⁰
3. 120⁰
4. 105⁰
5. 95⁰
6. 30⁰
7. 36⁰
8. 130⁰
9. 12
10. 11
11. 4
12. 12
13. 3
14. 3
15. 40⁰
16. 38⁰
17. 75⁰
18. 140⁰