Back to: Geometry
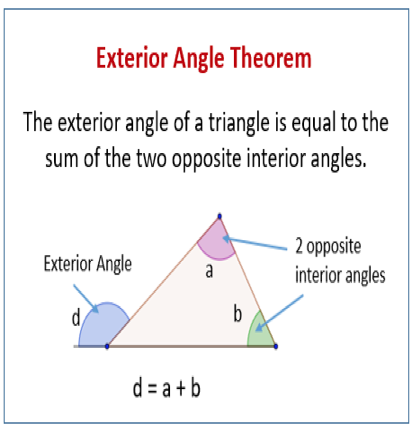
An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side.
- The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
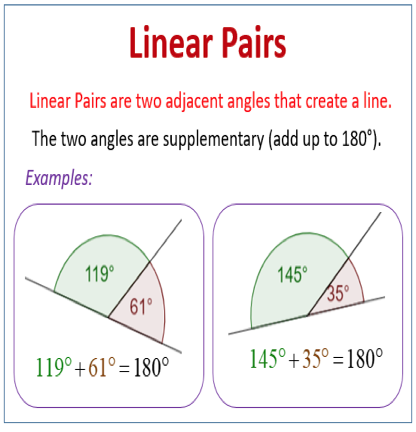
- The exterior angle and the adjacent angle next to it form a Linear Pair (sum to 1800).
Example 1
Find the value of the missing angles.
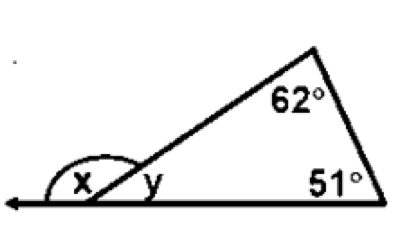
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Therefore, x = 620 + 510 = 1130.
The exterior angle and the adjacent angle next to it form a Linear Pair (sum to 1800).
Therefore, x + y = 1800. Then, y = 1800 – 113 = 670.
Example 2
Find the value of the missing angles.
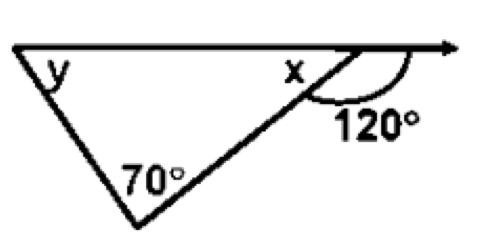
x = 1800 – 1200 = 600.
y = 1200 – 700 = 500.
Example 3
Find the value of the missing angles.
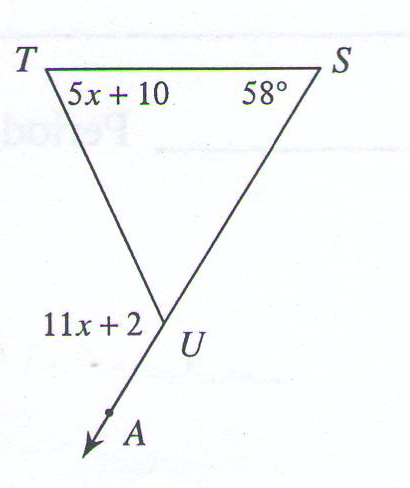
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Then, 11x + 2 = (5x + 10) + 58
11x + 2 = 5x + 68
– 5x – 2 = -5x – 2
———————–
6x = 66
x = 11
Therefore, 11x + 2 = 11(11) + 2 = 123. (angle AUT)
Also, 5x + 10 = 5(11) = 10 = 65 (angle T)
And 180 – 123 = 57 (angle TUS)
Solve the following problems.
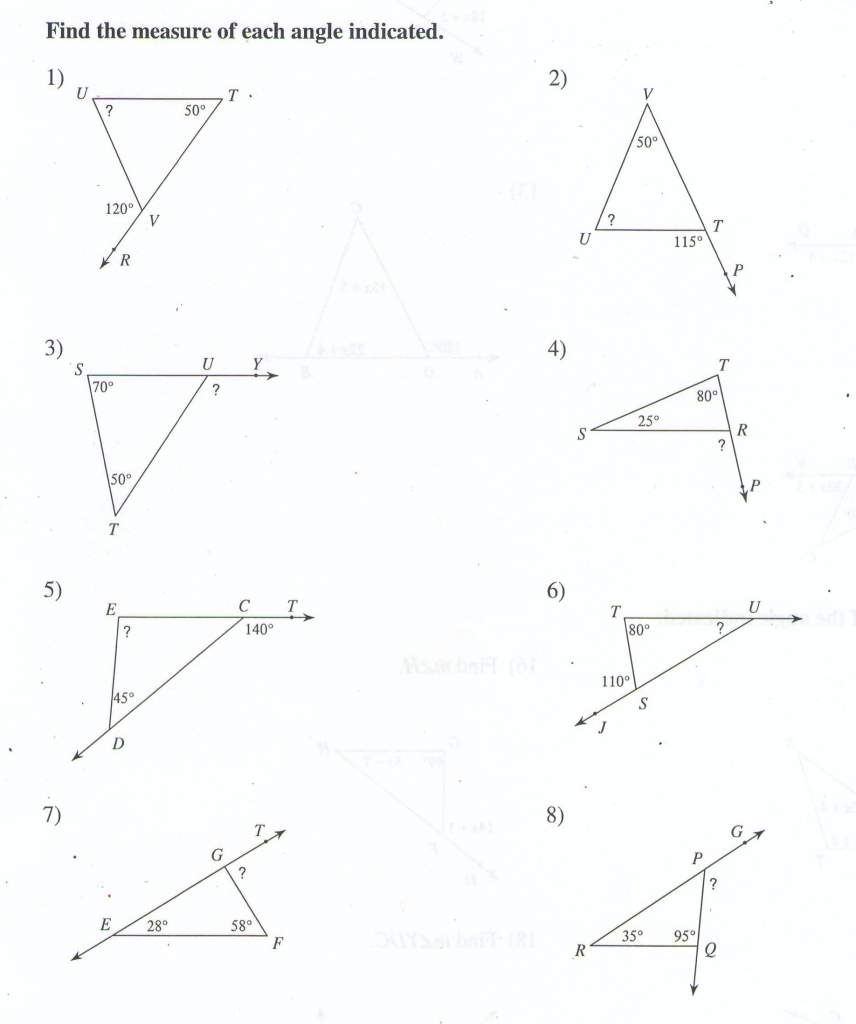
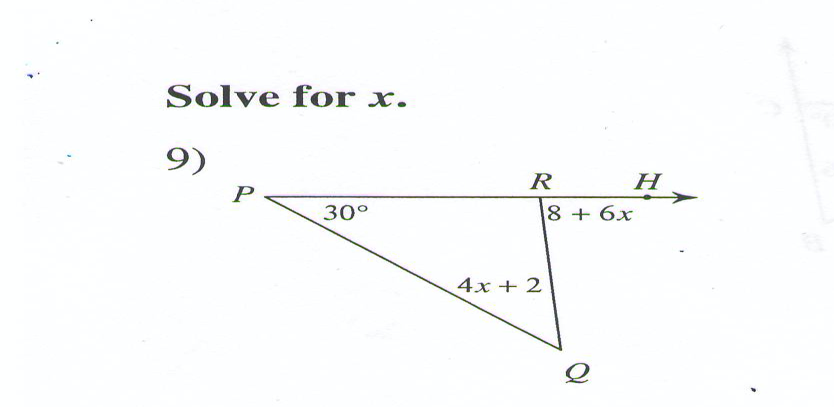
Solve for all the missing angles.
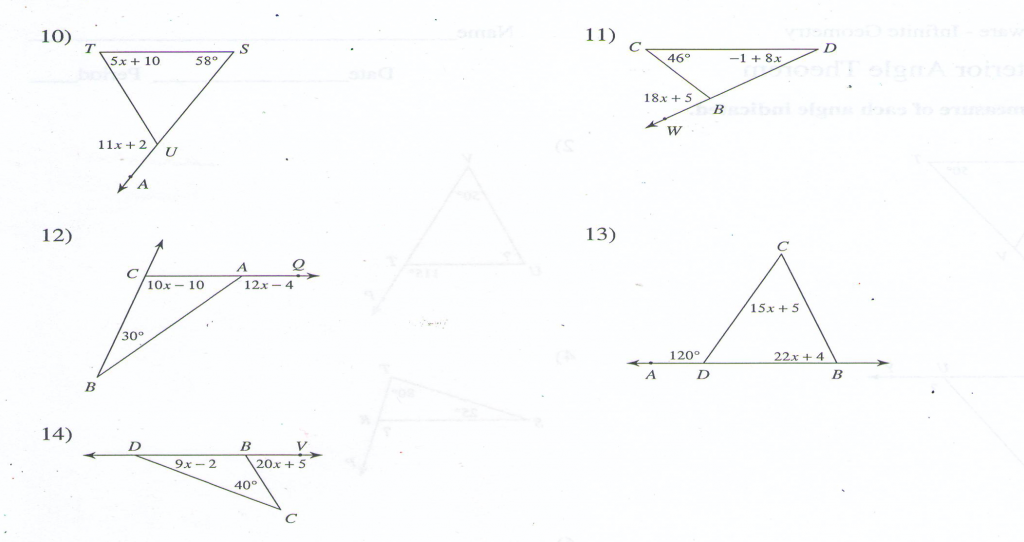
SOLUTIONS
- 700
- 650
- 1200
- 1050
- 950
- 300
- 360
- 1300
- 12
- 11
- 4
- 12
- 3
- 3
- 400
- 380
- 750
- 1400
